为什么CNN反向传播计算梯度时需要将权重旋转180度
CNN最近在计算机领域遍地开花,最基础的图像分类,目标检测,图像分割,跟踪,边缘检测等Topic的桥头堡都插上了CNN的大旗,在CNN不断刷新传统方法的结果时,我们需要深入的理解CNN的原理。
CNN最主要的就是梯度优化算法,正向传播,反向梯度传播更新权重。具体的推导和演示请看我前面的博客http://manutdzou.github.io/2016/05/15/CNN-backpropagation.html。如果你深入理解算法原理会发现一个很怪异的地方,在反向计算梯度时需要将卷积核的权重旋转180度?为什么呢?这个问题起初也困扰我很久,现在作详细地解释。
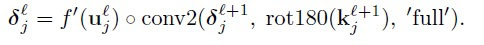
上述公式表示第$j$层feature map的$\delta$等于第$j+1$层的feature map的$\delta$和第$j+1$层的卷积核旋转180度后作卷积再乘以第$j$层feature map的激发函数。
由于卷积操作等于翻转180度后的相关操作,因此表述成CNN前向卷积,反向相关运算。在这再一次被数学的精妙所吸引啊,大自然的对偶关系真是造物主的神迹,咳咳,跑题了。。。
为什么要翻转卷积核呢?其实本质上还是BP算法。
在多层感知器中计算$\delta$误差如下:
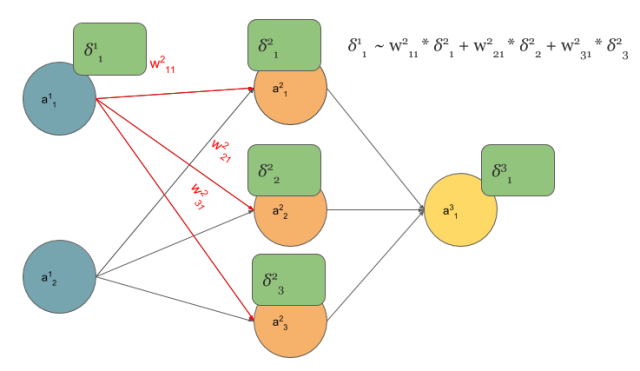
前层节点的$\delta$等于和该层节点相连接的$w$和后层节点的$\delta$相乘。BP算法的本质就是梯度链式求导。
那如何将多层感知器的求导规则对应卷积网络的推导呢?卷积网络本质上也是多层感知器,只是有了感受野和权值共享。
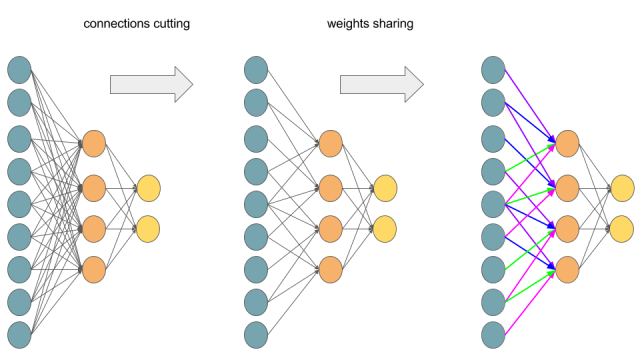
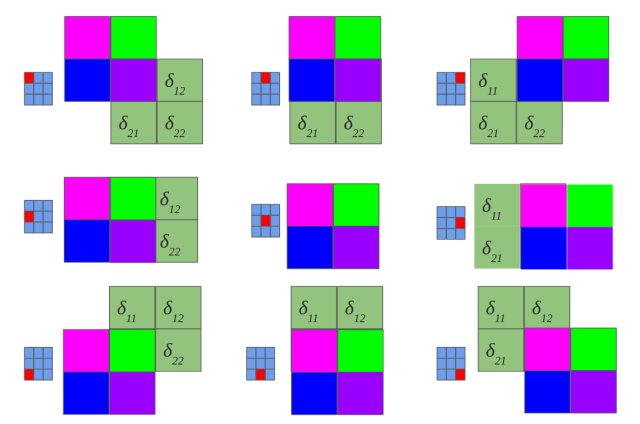
如上图将全连接的多层感知器改成权值共享的卷积网络。上图表示一个$3\times 3$的feature map和$2\times 2$的卷积核卷积,如果你还看不出来那下面一个图将完全展示上图的过程:
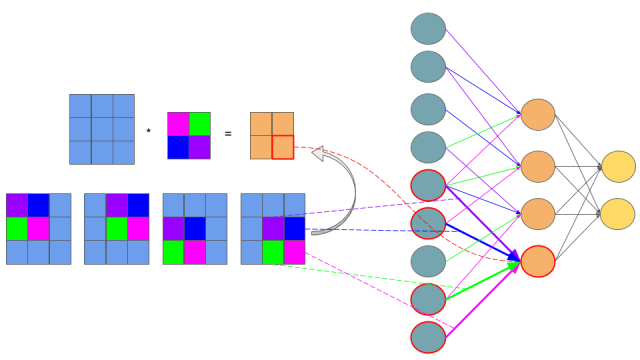
由于卷积操作等于翻转180度后的相关,所以需要将卷积核上下左右翻转,所以一共就输出4个节点,每个节点是一次相关操作,每个节点和对应颜色卷积核参数的连接情况非常清楚了。
展开成为MLP以后你应该会计算梯度传播了吧,就是BP算法。
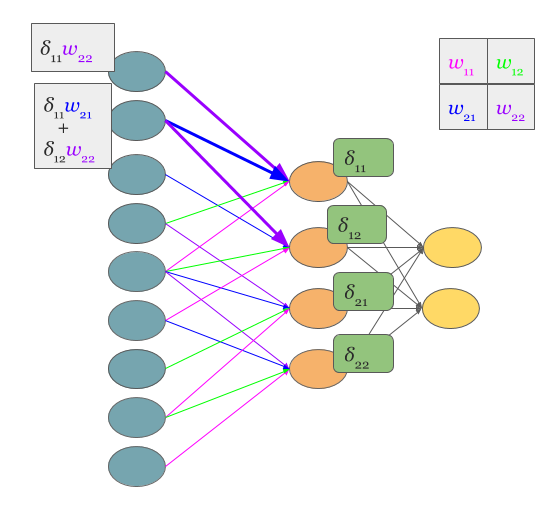
假设卷积后的feature map的$\delta$为$\delta_{11}$,$\delta_{12}$,$\delta_{21}$,$\delta_{22}$,所以根据链式求导规则不考虑激发函数,前一层第一个节点的$\delta$值为$\delta_{11}w_{22}$,第二个节点的的$\delta$值为$\delta_{11}w_{21}+\delta_{12}w_{22}$,如下图
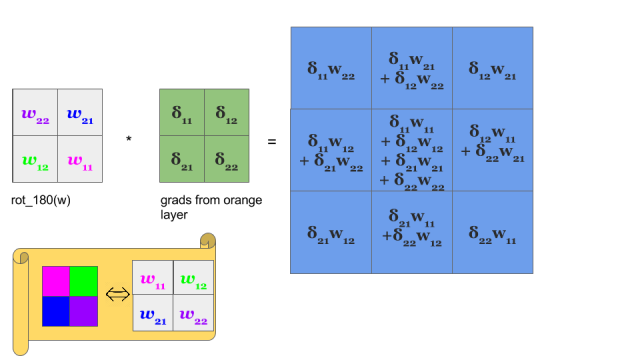
由上图可以看出前一层feature map的$\delta$正好等于后一层feature map的$\delta$和翻转180度后的卷积核做卷积(吐槽下我都觉得叙述的好拗口,但这就是真理啊)。
所以如果前向卷积核是做卷积,则后向传播算feature map的$\delta$时候卷积核做翻转后的卷积(或者叫相关);如果前向卷积核是做相关,则后向传播算feature map的$\delta$时候卷积核做翻转后的相关(或者叫卷积)!有的库用相关实现,有的库用卷积实现,本质上都是一样的,而且这里的卷积都是指严格意义上的离散卷积。卷积神经网络也可以叫做相关神经网络,只是卷积神经网络听上去可能更高大上一点吧。
理论推导
警示:前方高能
在传统的MLP中,对于一个神经元
\[\delta_{j}^{l}=\frac{\partial C}{\partial z_{j}^{l}}\]其中$z_{j}^{l}$定义为
\[z_{j}^{l}=\sum_{k}w_{jk}^{l}a_{k}^{l-1}+b_{j}^{l}\]$a_{j}^{l}=\sigma \left ( z_{j}^{l} \right )$是当前层的激发函数,可以是sigmoid, hyperbolic tangent or relu
将MLP替换为Convolutions将$z_{j}$替换为$z_{x,y}$:
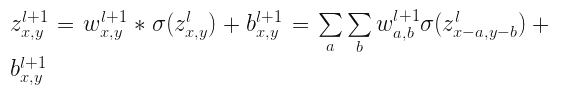
这是一个标准的CNN前向传播时候的写法,并且根据卷积定理转换为相关运算。同样error对$l$层求倒数:

其中$z_{x,y}^{l}$和 $z_{x{}’,y{}’}^{l+1}$连接,将上式写成如下形式:
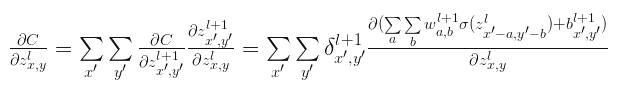
第一项为定义的$l+1$层的$\delta$,第二项展开以后变的很大,我们不需要惧怕这样一个大怪兽,其中很多分量求导后都等于0,只有那些以$x=x{}’-a$和$y=y{}’-a$的分量导数不为0。所以最后写成:
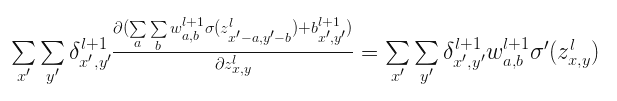
将$a=x{}’-x$和$b=y{}’-y$替换,则上式写成
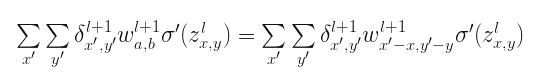
上述式子是卷积的相关表示形式,也可以写成:
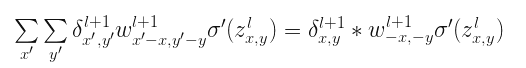
这不是很眼熟?如果写成:
\[ROT180\left ( w_{x,y}^{l+1} \right )=w_{-x,-y}^{l+1}\]这不正是翻转的卷积核么。
最后更新权重的$\delta$
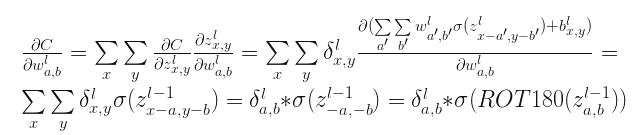
也就是卷积核的权重$\delta$等于当前层feature map的$\delta$和前一层feature map的值旋转180度后作卷积或者表述为卷积核的权重$\delta$等于当前层feature map的$\delta$和前一层feature map的值作相关
看我写的辛苦求打赏啊!!!有学术讨论和指点请加微信manutdzou,注明

