Transposed Convolution, Fractionally Strided Convolution or Deconvolution
反卷积(Deconvolution)的概念第一次出现是Zeiler在2010年发表的论文Deconvolutional networks中,但是并没有指定反卷积这个名字,反卷积这个术语正式的使用是在其之后的工作中(Adaptive deconvolutional networks for mid and high level feature learning)。随着反卷积在神经网络可视化上的成功应用,其被越来越多的工作所采纳比如:场景分割、生成模型等。其中反卷积(Deconvolution)也有很多其他的叫法,比如:Transposed Convolution,Fractional Strided Convolution等等。
卷积层
卷积层大家应该都很熟悉了,为了方便说明,定义如下:
二维的离散卷积($N=2$)
方形的特征输入($i_{1}=i_{2}=i$)
方形的卷积核尺寸($k_{1}=k_{2}=k$)
每个维度相同的步长($s_{1}=s_{2}=s$)
每个维度相同的padding ($p_{1}=p_{2}=p$)
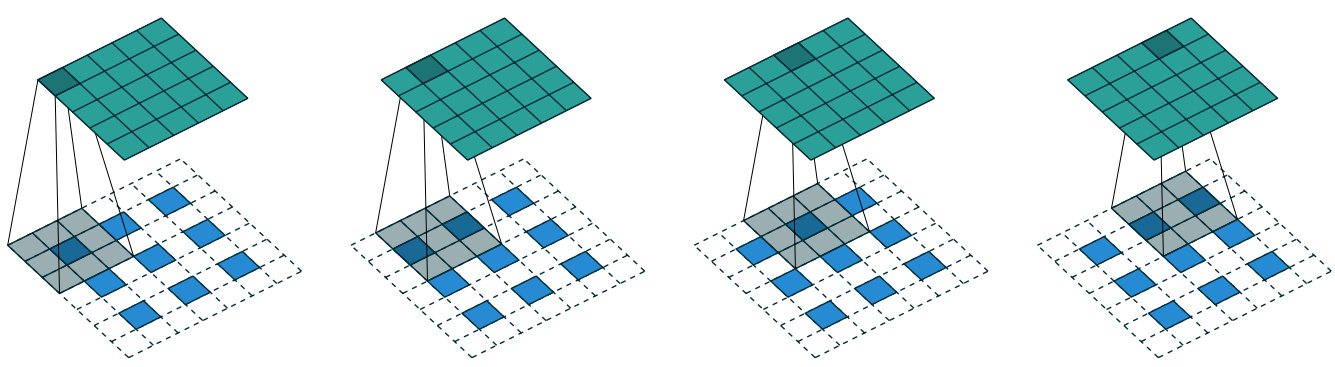
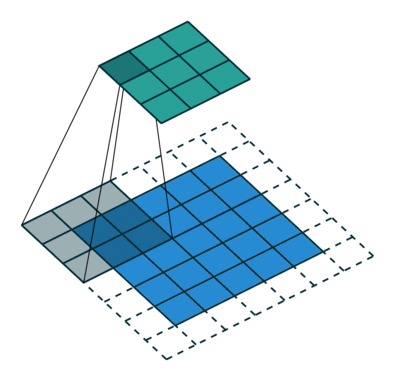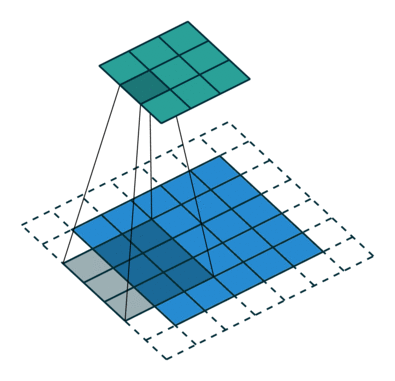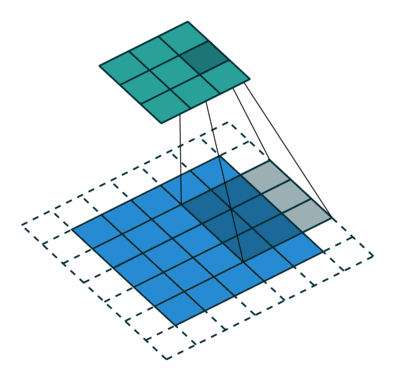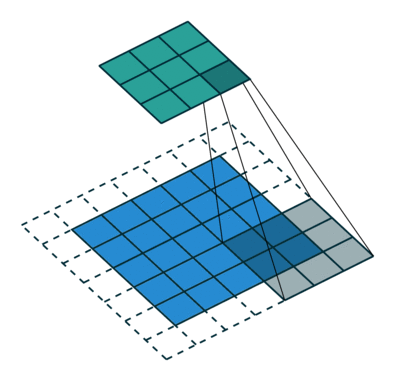
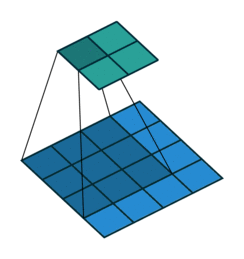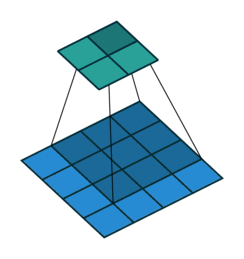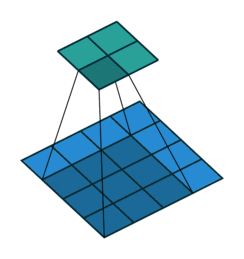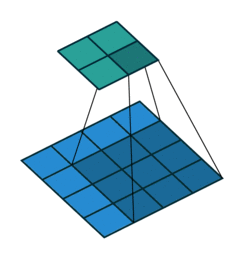
下图表示参数为 ($i=5,k=3,s=2,p=1$) 的卷积计算过程,从计算结果可以看出输出特征的尺寸为 ($o_{1}=o_{2}=o=3$)。
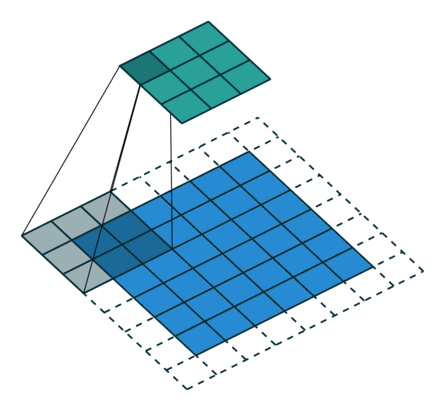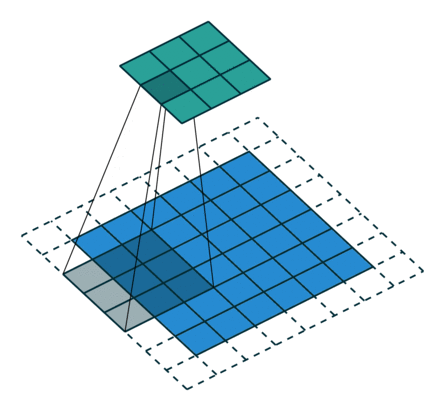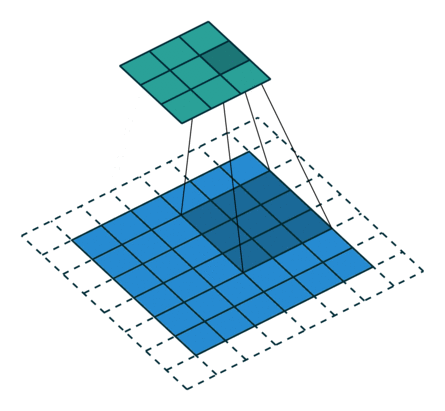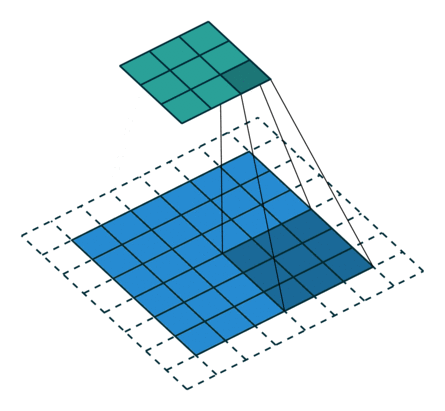
下图表示参数为 ($i=6,k=3,s=2,p=1$) 的卷积计算过程,从计算结果可以看出输出特征的尺寸为 ($o_{1}=o_{2}=o=3$)。
从上述两个例子我们可以总结出卷积层输入特征与输出特征尺寸和卷积核参数的关系为:
\[o=\left [ \frac{i+2p-k}{s} \right ]+1\]其中$\left [ x \right ]$表示对 $x$ 向下取整。
反卷积层
在介绍反卷积之前,我们先来看看卷积运算和矩阵运算之间的关系。
卷积和矩阵相乘
考虑如下一个简单的卷积层运算,其参数为 ($i=4,k=3,s=1,p=0$),输出 $o=2$。
对于上述卷积运算,我们把上图所示的3×3卷积核展成一个如下所示的[4,16]的稀疏矩阵 $C$, 其中非0元素 $w_{i,j}$ 表示卷积核的第 $i$ 行和第 $j$ 列。
$\begin{pmatrix} w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0 & 0 \ 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 \ 0 & 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} \ \end{pmatrix}$
我们再把$4\times4$的输入特征展成$\left [ 16,1\right ]$的矩阵 $X$,那么 $Y=CX$ 则是一个$\left [ 4,1\right ]$的输出特征矩阵,把它重新排列$2\times2$的输出特征就得到最终的结果,从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是,在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的,因为这个转换会存在很多无用的0乘操作.
通过上述的分析,我们已经知道卷积层的前向操作可以表示为和矩阵$C$相乘,那么我们很容易得到卷积层的反向传播就是和$C$的转置相乘。
反卷积和卷积的关系
前面我们已经说过反卷积又被称为Transposed(转置) Convolution,我们可以看出其实卷积层的前向传播过程就是反卷积层的反向传播过程,卷积层的反向传播过程就是反卷积层的前向传播过程。因为卷积层的前向反向计算分别为乘 $C$ 和 $C^{T}$,而反卷积层的前向反向计算分别为乘 $C^{T}$ 和 $(C^{T})^{T}$ ,所以它们的前向传播和反向传播刚好交换过来。
下图表示一个和上图卷积计算对应的反卷积操作,其中他们的输入输出关系正好相反。如果不考虑通道以卷积运算的反向运算来计算反卷积运算的话,我们还可以通过离散卷积的方法来求反卷积(这里只是为了说明,实际工作中不会这么做)。
同样为了说明,定义反卷积操作参数如下:
二维的离散卷积($N=2$)
方形的特征输入($i_{1}^{‘}=i_{2}^{‘}=i^{‘}$)
方形的卷积核尺寸($k_{1}^{‘}=k_{2}^{‘}=k^{‘}$)
每个维度相同的步长($s_{1}^{‘}=s_{2}^{‘}=s^{‘}$)
每个维度相同的padding ($p_{1}^{‘}=p_{2}^{‘}=p^{‘}$)
下图表示的是参数为( $i^{‘}=2,k^{‘}=3,s^{‘}=1,p^{‘}=2$)的反卷积操作,其对应的卷积操作参数为 ($i=4,k=3,s=1,p=0$)。我们可以发现对应的卷积和非卷积操作其 ($k=k^{‘},s=s^{‘}$),但是反卷积却多了$p^{‘}=2$。通过对比我们可以发现卷积层中左上角的输入只对左上角的输出有贡献,所以反卷积层会出现 $p^{‘}=k−p−1=2$。通过示意图,我们可以发现,反卷积层的输入输出在 $s=s^{‘}=1$的情况下关系为:
\[o^{'}=i^{'}−k^{'}+2p^{'}+1=i^{'}+(k−1)−2p\]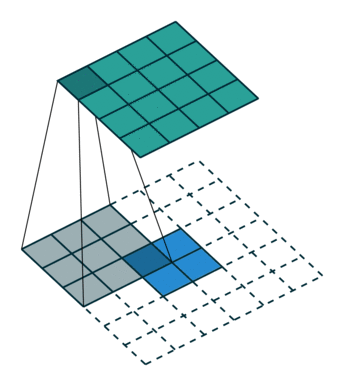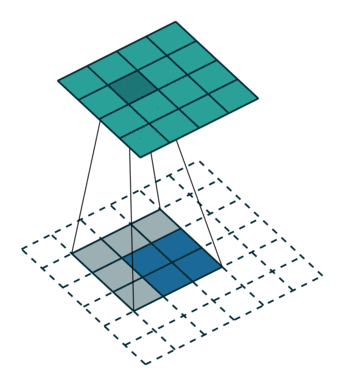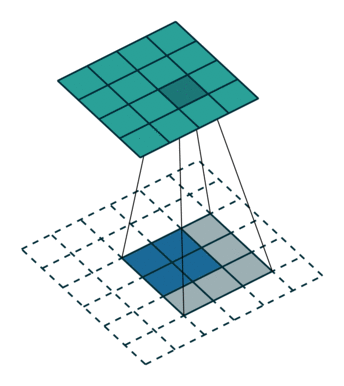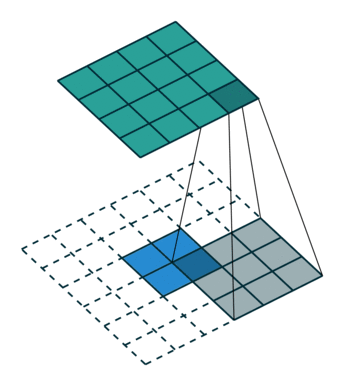
Fractionally Strided Convolution
上面也提到过反卷积有时候也被叫做Fractionally Strided Convolution,翻译过来大概意思就是小数步长的卷积。对于步长 $s>1$的卷积,我们可能会想到其对应的反卷积步长 $s^{‘}<1$。 如下图所示为一个参数为 $i=5,k=3,s=2,p=1$的卷积操作(就是第一张图所演示的)所对应的反卷积操作。对于反卷积操作的小数步长我们可以理解为:在其输入特征单元之间插入 $s−1$ 个$0$,插入$0$后把其看出是新的特征输入,然后此时步长 $s^{‘}$ 不再是小数而是为$1$。因此,结合上面所得到的结论,我们可以得出Fractionally Strided Convolution的输入输出关系为:
\[o^{′}=s(i^{'}−1)+k−2p\]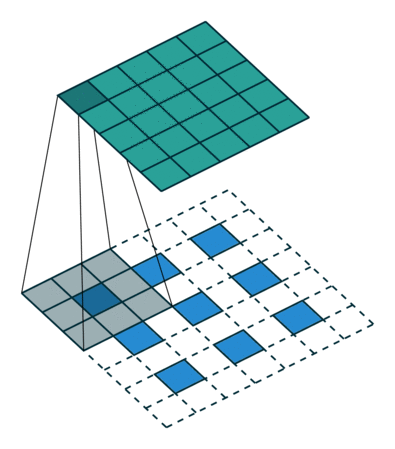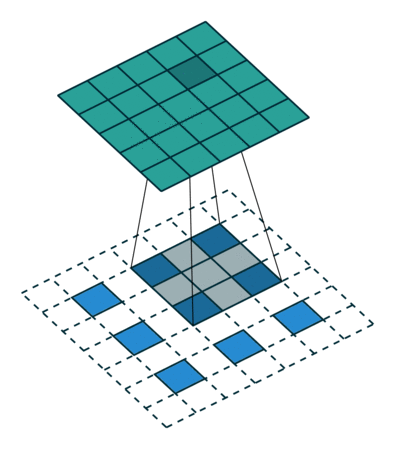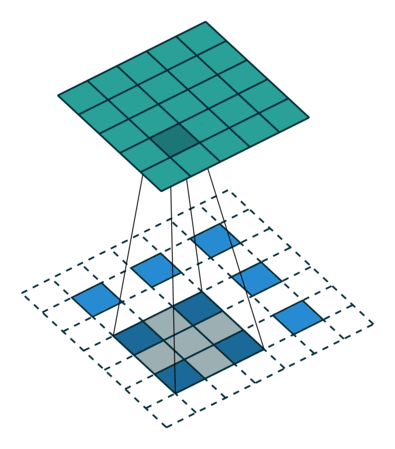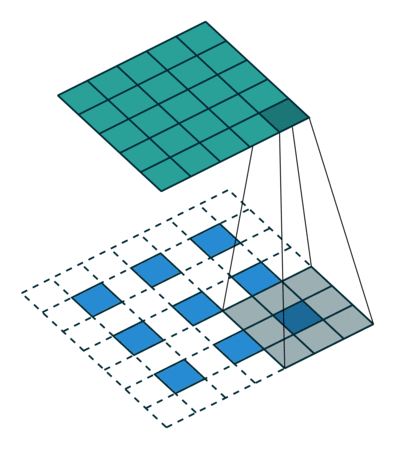
看我写的辛苦求打赏啊!!!有学术讨论和指点请加微信manutdzou,注明

