RNN的数学推导

含有一个隐层的RNN结构如下：

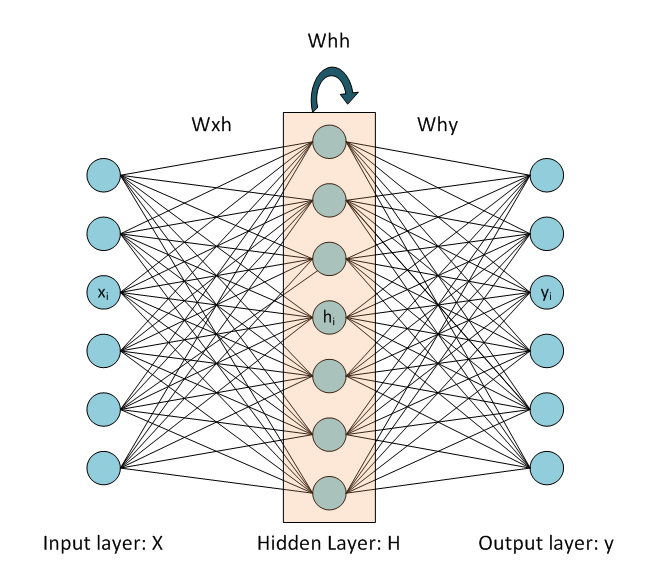
RNN的前馈传播python代码如下：

class RNN:
  # ...
  def step(self, x):
    # update the hidden state
    self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
    # compute the output vector
    y = np.dot(self.W_hy, self.h)
    return y

其中，$t$ 时刻的隐层状态的计算公式为：$h^{t}=tanh\left ( Whh\ast h^{t-1}+Wxh\ast x^{t} \right )$,$x^{t}$ 表示 $t$ 时刻RNN的输入。需要注意的是这里的RNN的hidden layer采用了tanh作为激活函数（Activation function）, Output layer则没有采用任何激活函数，即为线性的output.

利用RNN前馈传播作预测

我们利用RNN来进行下一个character的预测，利用已知的字母序列来预测下一个可能出现的字母，首先我们有以下若干RNN使用的假设，用来初始化我们的RNN模型：

1. 假设我们一共有V个character, 即字典的大小为V，那么RNN的输入为one hot vector, dim=V

2. 假设我们当前的RNN的hidden layer的size为H,则我们的RNN的权重矩阵的维度分别为：

a. $Wxh:H\ast V$, input to hidden layer weight

b. $Whh:H\ast H$, hidden to hidden layer weight

c. $Why:V\ast H$, hidden to output layer weight

3. Output layer的维度为V，输出为每个字母可能出现的概率，output layer做了一个softmax操作，获得每个字母可能出现的概率分布，在预测下一个字母的时候就可以在这个得到的字母分布的基础上进行采样。

4. 设Hidden layer的输入为$u$,输出为$h$, output layer的输入为$u{}’$,因为hidden layer采用tanh作为激活函数,所以$h=tanh\left ( u \right )$,output layer没有采用激活函数，所以$y=u{}’$.

接下来我们讲的所有的操作，forward propagation & back propagation都是以本节的设定为基础的。

损失函数

在NN中常用的两种Loss function有：Sum of squared error (Quadratic error) & cross entropy error。 假设$t$为训练样本的真实值，$y$为神经网络的输出，我们的训练样本为$\left ( x,t \right )$，一个样本。我们下面的公式也是针对一个样本而言，对于所有的样本也就很简单了。

Sum of Squared error (Quadratic error)

当神经网络的output layer没有采用激活函数的时候，我们应该采用Quadratic error，这样能够比较快速的进行梯度下降参数估计。

Cross Entropy Error

如果当output layer采用sigmoid激活函数的时候，我们应该采用cross entropy error进行参数估计，这是因为如果采用sigmoid激活函数，采用cross entropy error能够在求导的时候消掉sigmoid函数，这样能够加快梯度下降的速度。接下来的参数估计推导部分会有详细的推导说明。如果output layer没有采用sigmoid函数，但是却使用cross entropy error来进行参数估计，那么就会得到不是很舒服的偏导数公式，可能对梯度下降的速度有所影响。

反向传播

前向传播的计算过程如下：

上面的计算公式中，具体的每个神经元的计算如下：

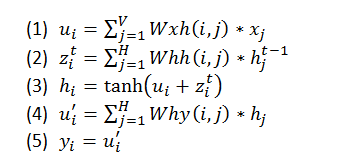
Quadratic Error VS Cross Entropy Error

在这里只考虑一个训练样本时候误差对输出层的导数，多个样本时候只需要求和就行

Quadratic error function：$E=\frac{1}{2}\left ( t-y \right )^{2}$

Cross entropy error: $E\left ( t,y \right )=-\left [ tln\left ( y \right )+\left ( 1-t \right )ln\left ( 1-y \right )\right ]$

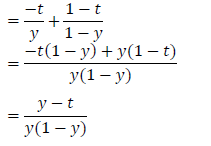
因为output layer没有采用激活函数，所以输出层的输入值的误差导数和$\frac{\partial E}{\partial u{}’}$一样

所以当NN中Output layer没有激活函数的时候采用Quadratic error的trick.

误差对输出层输入值的导数

(A)Linear output layer

如果output layer 没有激活函数，那么就如上面得到的一样:$\frac{\partial E}{\partial u{}’}=\frac{\partial E}{\partial y}$,那针对不同的cost function就对应不同的公式。

(B)Sigmoid output layer

假如我们的output layer采用sigmoid激活函数，那么我们来证明一下为什么使用cross entropy error能够是参数估计收敛的更快。

让我们计算输出层的误差对输入层的导数，假设输出层的输入值是$z$,这里$z=u{}’$,$y=sigmoid\left ( z \right )$.

在NN中，输出层的误差和输出层的输入值的误差是守恒的。我们用$\delta^{L}$表示输出层的误差.

首先，sigmoid函数的导数为：

然后我们计算输出层的输入值的导数：

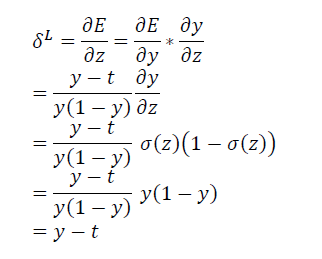
可见如果用的sigmoid激发函数，利用cross entropy error可以将sigmoid函数消掉，在利用cross entropy error进行梯度下降参数更新时候能够避免sigmoid函数最后迭代速度减慢。

反向传播推导

在进行参数估计的时候我们采用Quadratic Error：$E=\frac{1}{2}\left ( t-y \right )^{2}$来衡量当前的系统误差并进行梯度下降计算。

计算输出层的梯度误差值

矩阵化得到：

计算输出层的输入值的梯度误差值

因为output layer没有采用任何激活函数，为linear output，所以$u_{i}{}’=y_{i}$, 那么偏导数也是一样的，如下：

矩阵化得到：

计算隐藏层和输出层之间权重的梯度

已知 $u_{i}{}’=\sum_{j=1}^{H}Why\left ( i,j \right )\ast h_{j}$

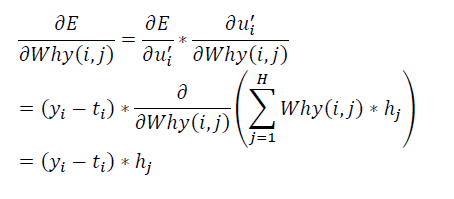
这里，公式中的$\frac{\partial E}{\partial u_{i}{}’}$已经计算得到，矩阵化上面公式得到：

计算隐藏层输出节点的梯度

隐藏层$h$受到两个公式影响，所以计算关于$h$的偏导数的时候，需要将这两个公式都计算关于$h$的偏导数。

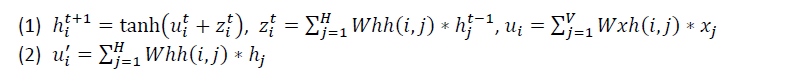
上面的公式(1)如果考虑tanh括号中的项，还可以写成：$u_{i}^{t+1}=u_{i}^{t}+z_{i}^{t}$,矩阵化表示就是：

因为在RNN存在hidden layer 到hidden layer的计算，在计算$h^{t+1}$的时候用到了$h^{t}$, 所以在计算偏导数时要加上来自下一个时刻$t+1$时针对$u$的误差的偏导数，即将$t+1$时刻的hidden layer的输入的误差反向传播到t时刻的输出误差。也可以理解为依赖于$h^{t}$的变量有$u^{t+1}$。

我们将下一时刻的hidden layer的input 的关于误差的偏导数称为 dnext，然后计算下面的关于误差的针对output of hidden layer的偏导数。

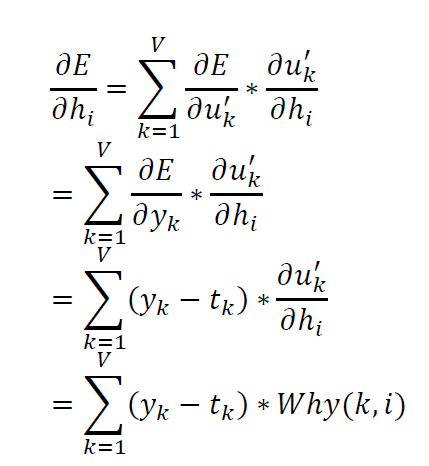
这里$u_{i}{}’=\sum_{j=1}^{H}Whh\left ( i,j \right )\ast h_{j}$,并且$\frac{\partial E}{\partial y_{k}}$已经计算得到

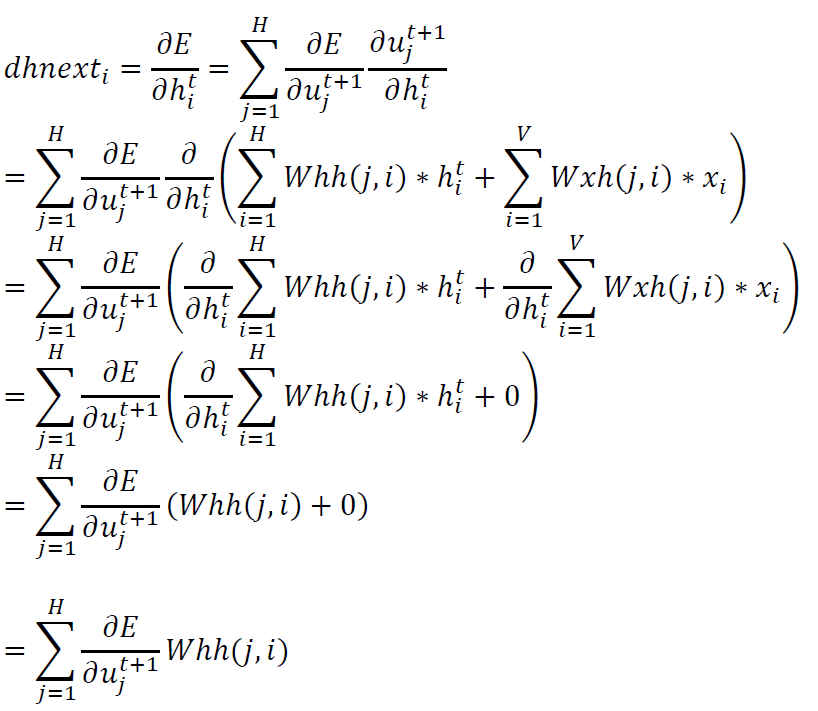
矩阵化后得到：

注意上面公式中的$\frac{\partial E}{\partial u_{j}^{t+1}}$暂时还没有计算得到，在下一步计算中会计算。

矩阵化上面两个公式得到：

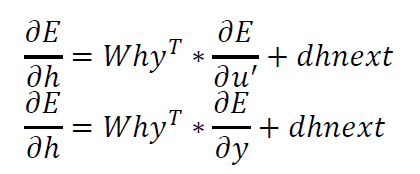
计算隐藏层输入节点的导数

我们称隐藏层的输入的误差偏导数为hraw,则

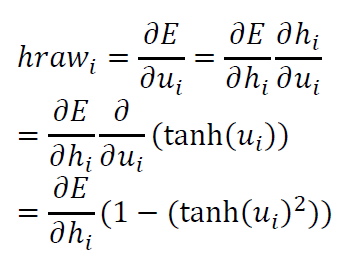
其中$\frac{\partial E}{\partial h_{i}}$已经得到，并且$\frac{\partial h_{i}}{\partial u_{i}}=1-\left ( tanh\left ( u_{i} \right )\right)^{2}$,因为隐藏层采用了tanh作为激活函数，$h_{i}=tanh\left ( u_{i} \right )$,$tanh\left ( x \right )$的导数为$1-\left ( tanh\left ( x \right ) \right )^{2}$.

矩阵化得到：

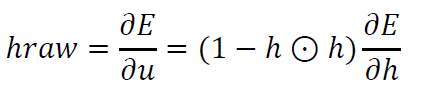
其中$\odot $表示点乘操作。

计算输入层和隐藏层权重的导数

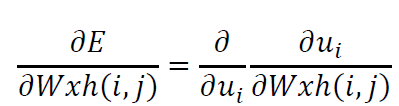
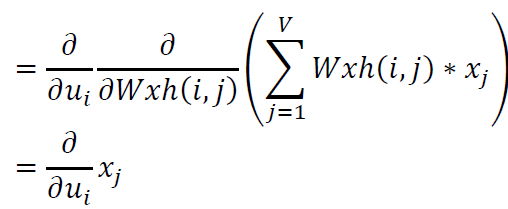
这里，已知$u_{i}=\sum_{j=1}^{V}Wxh\left ( i,j \right )\ast x_{j}$,矩阵化得到：

计算隐层和隐层间时序的权重导数

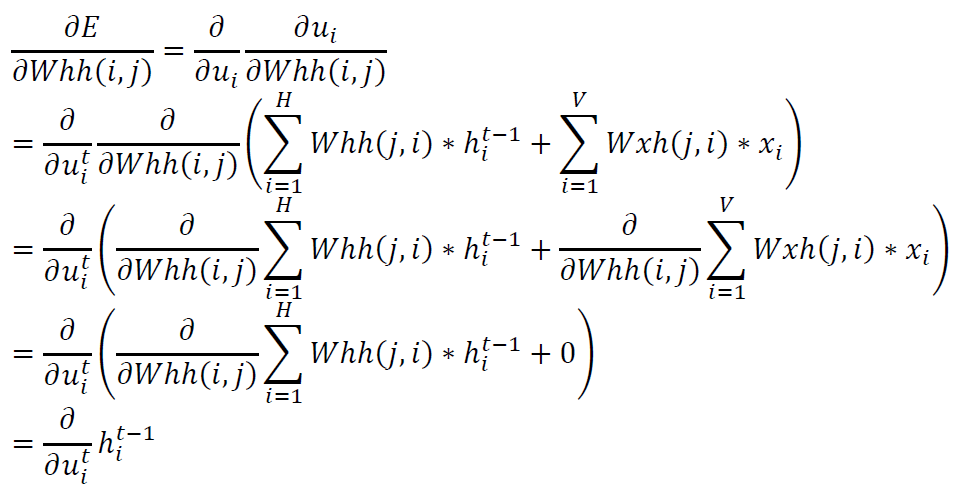
这里，$u_{i}^{t}=\sum_{i=1}^{H}Whh\left ( j,i \right )\ast h_{i}^{t-1}+\sum_{i=1}^{V}Wxh\left ( j,i \right )\ast x_{i}$,矩阵化得到：

到目前为止，我们已经计算得到了所有的参数矩阵关于误差的偏导数，然后就可以根据偏导数进行梯度下降进行参数更新了。

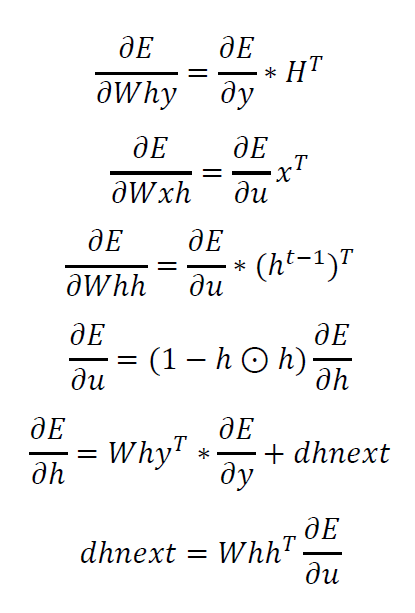
其中dhnext在计算过程中，初始化为0.

由此可见其实RNN的推导相比于CNN要简单好多，可以理解为是一个普通全连接的网络连接的梯度传递和隐层的时序连接的梯度传递的和。

看我写的辛苦求打赏啊！！！有学术讨论和指点请加微信manutdzou,注明