深度学习中的稀疏编码思想
正则回归模型
研究生阶段主要从事稀疏编码的科研工作,在特征表示阶段,稀疏编码的特征能获得非常好的特征。稀疏编码主要通过编码方式在字典集上重构表征信号获得编码系数。如今深度学习统治机器学习,但是从来没有一个东西是横空出世的,算法是一路传承下来的,算法中的思想都是有关联的,下面研究下深度学习和稀疏编码的数学内在联系。
机器学习里典型的带正则项的回归模型可以表示为:
\[Y=argmin\left \| X-DY \right \|^{^{2}}+\gamma \left ( Y \right )\]其中$X$是输入数据,$Y$是求解的编码系数,$D$是字典基(basis),$Y$除了要求对于$D$能有很好重建$X$外,还受到一个额外的正则化项$\gamma \left ( Y \right )$的约束。这个模型看似简单,实则机器学习里众多著名的模型比如(PCA,LDA,Sparse Coding等)都可以用上述表达式表示。以上的算法可以写成一个迭代的一般表示形式:
\[Y^{k+1}=N\left ( L_{1}\left ( X \right )+L_{2}\left ( Y^{k} \right ) \right )\]$Y^{k}$是k-iteration的输出,$L_{1}$,$L_{2}$,$N$是三个变换算子。这一迭代算法可以等价表示成下图中带反馈系统的形式:
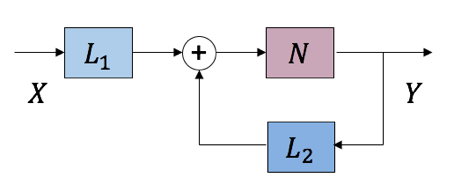
对于上图反馈循环形式,接着做前向展开,获得一个有无限个前向传播单元的级联结构,然后再将这个结构截断,获得一个固定长度的前向结构:
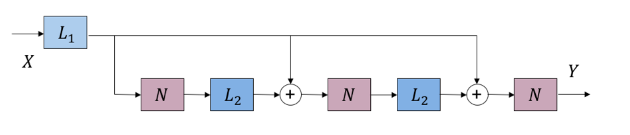
上图即是一个“展开截断”的前向结构示意图($k=2$)。首先这一结构避免了环形结构、反馈回路的出现,所有信息流都是前向的。其次。这一结构等价于将原有迭代算法做$k$次近似,获得一个有限固定迭代步数下“不精确”的回归解。有趣的是在很多例子中$L_{1}$和$L_{2}$是带参数的线性变换,而$N$是不带参数的非线性变换。这和DNN的结构形成了精妙的巧合对应;如果将$L_{1}$和$L_{2}$看做是DNN中可以训练的layer,$N$看做是DNN中的非线性激发或者pooling,那么“展开截断”后的嵌套结构完全可以看做一个$k+1$层,有一定特殊结构的DNN。
所以带卷积情况下的带正则项的回归问题为:
\[Y=argmin\left \| X-\sum_{i}F_{i}\ast Z \right \|^{2}+\sum_{i}\gamma \left ( Z_{i} \right )\]这一问题的形式,解法和结论都和前面的线性回归模型相仿。事实上,线性回归模型的结论将自然对应DNN的全连接层,而卷积回归模型的结论将对应到DNN的卷积层。
深度网络中潜藏的稀疏表示
现在我们考虑引入1范数约束的稀疏性作为回归模型的正则项:
\[Y=argmin\left \| X-DY \right \|^{2}+c\left \| Y \right \|_{1}\]上式是经典的稀疏表示问题。对应的迭代算法形式如下:
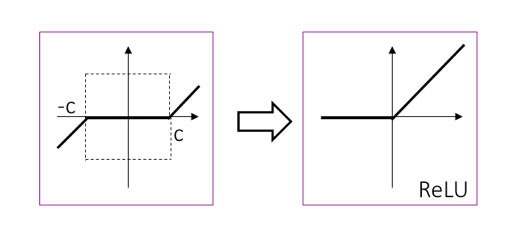
\[Y^{k+1}=N\left ( L_{1}\left ( X \right )+L_{2}\left ( Y^{k} \right ) \right ),L_{1}\left ( X \right )=D^{T}X,L_{2}\left ( Y^\left ( k \right )\right )=\left ( I-D^{T}D \right )Y^\left ( k \right )\]则是著名的软门限算子,形式如下图左所示,这很容易联想到DNN中最成功的ReLU(Rectified Linear Unit)激活函数,形式如下图右。
既然ReLU很强大,所以加入稀疏框架中,对$Y$加一个非负约束:
\[Y=argmin\left \| X-DY \right \|^{2}+c\left \| Y \right \|_{1},Y\geq 0\]这一约束的直接效果是把软门限算子的负半侧砍掉归0。进一步,我们可以把原本软门限算子中的门限参数c,移到线性变换当中。最后迭代形式里:
\[L_{1}\left ( X \right )=D^{T}X,L_{2}\left ( Y^\left ( k \right )\right )=\left ( I-D^{T}D \right )Y^{k},N=ReLU\]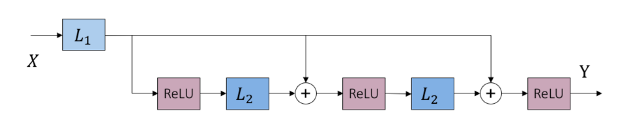
一个小问题:为什么可以“硬凑”一个非负约束到原稀疏表示问题中呢?首先“哲学”上,稀疏表达将“部分”线性组合为“整体”,如果这些“部分”还会相互抵消,总觉得不太自然,当然此属怪力乱神,不听也罢。不过生物建模上,其实早将稀疏表达和神经元编码联系了起来:稀疏特征的值对应于神经元的“激发率”(firing rate, i.e., the average number of spikes per unit time),自然而然需要非负。另外,图像处理和计算机视觉的研究者,很多都熟悉非负稀疏编码(nonnegative sparse coding, NSC)的大名;此前NSC 亦是学习视觉特征的最成功方法之一。如今风水轮流转,DNN大火,经过各种神经元的经验化设计尝试、大浪淘沙,ReLU脱颖而出 。而从前的非负性和稀疏性假设经过改头换面,又于无意识间悄悄潜伏进了ReLU中;这不能不说是个有趣的发现。
再进一步,上面那个对应非负稀疏编码的“展开&截断”前向结构,如果我们想避免那些不“特别典型”的中间连接(事实上,这些“捷径”的设计正在成为DNN的新热点,参加ResNet等工作)和权重共享(被重复展开),一个选择是只保留最开始的一部分计算而删掉后面,即让迭代算法从初始值开始只跑一步近似:
\[Y=ReLU\left ( D^{T}X-c \right )\]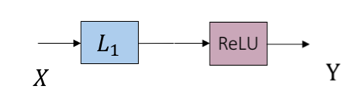
如此便获得了DNN中最典型的构成单元:全连接层 + 偏置 + 神经元ReLU。偏置 来源于原本1范数正则项的加权;在原优化问题中,调整c即调整Y的稀疏度。不难想到,如果将非负稀疏编码换成非负稀疏卷积编码,那么同样可以得到由卷积层 + 偏置 +神经元ReLU组成的单元。这一角度对一般DNN结构的分析提供了很多意味深长的提示。
最后,简单讲讲另外两种形式的稀疏性。其一是将稀疏编码中1范数换成0范数:
\[Y=argmin\left \| X-DY \right \|^{2}+c^{2}\left \| Y \right \|^{0}\]按照以上1范数情况下的推导结果,不难解出的形式为经典的硬门限算子(hard-thresholding)。相较软门限,硬门限容易获得零值更多、更稀疏的解,常有利于分类等任务。尤其有趣的是,这一算子在2015年的国际表示学习大会(ICLR)上被DNN研究者们“经验性”地设计出来,并被冠名以thresholded linear unit;实则未免稍稍有重造轮子之憾。另一个更有意义的例子是:
\[Y=argmin\left \| X-DY \right \|^{2} s.t. \left \| Y \right \|_{0}\leq M\]该问题中的约束条件可以看作池化算子(pooling):即将输入中绝对值最大的M个值保留、其余归0。考虑到0范数约束问题是特征选择的经典形式之一,这也让我们对原本被视作单纯工程“瞎凑”的池化操作的实际作用,有了更多遐想。
看我写的辛苦求打赏啊!!!有学术讨论和指点请加微信manutdzou,注明

