CNN反向求导及推导
首先我们来看看CNN系统的目标函数,设有样本$\left({x_i},{y_i} \right)$共$m$个,CNN网络共有L层,中间包含若干个卷积层和pooling层,最后一层的输出为$f\left( {x_i} \right)$,则系统的loss表达式为(对权值进行了惩罚,一般分类都采用交叉熵形式):
\[Loss=-\frac{1}{m}\sum_{i=1}^{m}y_{i}{}'logf\left ( x_{i} \right )+\lambda\sum_{k=1}^{L}sum\left ( \left \|W_{k} \right \|^{2} \right )\]问题一:求输出层的误差敏感项。
现在只考虑一个输入样本$\left( {x,y} \right)$的情形,loss函数和上面的公式类似是用交叉熵来表示的,暂时不考虑权值规则项,样本标签采用one-hot编码,CNN网络的最后一层采用softmax全连接(多分类时输出层一般用softmax),样本$\left( {x,y} \right)$经过CNN网络后的最终的输出用$f\left( {x} \right)$表示,则对应该样本的loss值为:
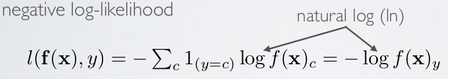
其中$f\left( {x} \right)$的下标$c$的含义见公式: \(f{\left( x \right)_c} = p\left( {y = c|x} \right)\)
因为$x$通过CNN后得到的输出$f\left( {x} \right)$是一个向量,该向量的元素值都是概率值,分别代表着$x$被分到各个类中的概率,而$f\left( {x} \right)$中下标c的意思就是输出向量中取对应$c$那个类的概率值。 采用上面的符号,可以求得此时loss值对输出层的误差敏感性表达式为:
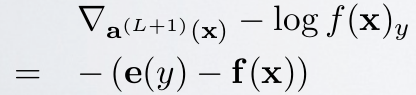
其中$e\left( y \right)$表示的是样本$x$标签值的one-hot表示,其中只有一个元素为1,其它都为0. 其推导过程如下(先求出对输出层某个节点c的误差敏感性,参考Larochelle关于DL的课件:Output layer gradient),求出输出层中c节点的误差敏感值:

由上面公式可知,如果输出层采用sfotmax,且loss用交叉熵形式,则最后一层的误差敏感值就等于CNN网络输出值$f\left( {x} \right)$减样本标签值$e\left( y \right)$,即$f\left( {x} \right)-e\left( y \right)$,其形式非常简单,这个公式是不是很眼熟?很多情况下如果model采用MSE的loss,即$loss=\frac{1}{2}\left ( e\left ( y \right ) -f\left ( x \right )\right )^{2}$,那么loss对最终的输出$f\left( {x} \right)$求导时其结果就是$f\left({x} \right)-e\left( y \right)$,虽然和上面的结果一样,但是大家不要搞混淆了,这2个含义是不同的,一个是对输出层节点输入值的导数(softmax激发函数),一个是对输出层节点输出值的导数(任意激发函数)。而在使用MSE的loss表达式时,输出层的误差敏感项为$\left ( f\left({x} \right)-e\left( y \right) \right ).*f\left ( x \right ){}’$,两者只相差一个因子。
这样就可以求出第L层的权值W的偏导数:
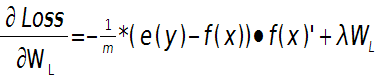
输出层偏置的偏导数:
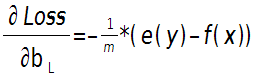
上面2个公式的$e\left( y \right)$和$f\left( {x} \right)$是一个矩阵,已经把所有$m$个训练样本考虑进去了,每一列代表一个样本。
问题二:当接在卷积层的下一层为pooling层时,求卷积层的误差敏感项。
假设第$l$(小写的$l$,不要看成数字’1’了)层为卷积层,第$l+1$层为pooling层,且pooling层的误差敏感项为:
\[\delta _{j}^{l+1}\]卷积层的误差敏感项为:
\[\delta _{j}^{l}\]则两者的关系表达式为:
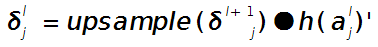
这里符号●表示的是矩阵的点积操作,即对应元素的乘积。卷积层和unsample()后的pooling层节点是一一对应的,所以下标都是用$j$表示。后面的符号
\[h\left ( a_{j}^{l} \right ){}'\]表示的是第$l$层第$j$个节点处激发函数的导数(对节点输入的导数)。
其中的函数unsample()为上采样过程,其具体的操作得看是采用的什么pooling方法了。但unsample的大概思想为:pooling层的每个节点是由卷积层中多个节点(一般为一个矩形区域)共同计算得到,所以pooling层每个节点的误差敏感值也是由卷积层中多个节点的误差敏感值共同产生的,只需满足两层见各自的误差敏感值相等,下面以mean-pooling和max-pooling为例来说明。 假设卷积层的矩形大小为4×4, pooling区域大小为2×2, 很容易知道pooling后得到的矩形大小也为2*2(本文默认pooling过程是没有重叠的,卷积过程是每次移动一个像素,即是有重叠的,后续不再声明),如果此时pooling后的矩形误差敏感值如下:
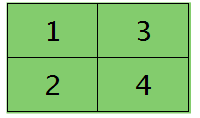
则按照mean-pooling,首先得到的卷积层应该是4×4大小,其值分布为(等值复制):
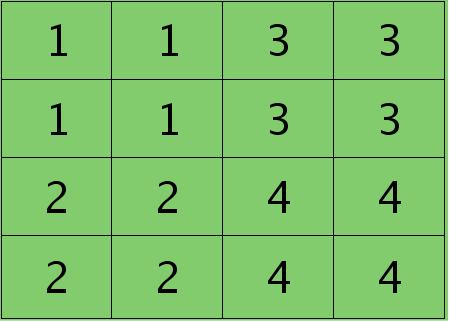
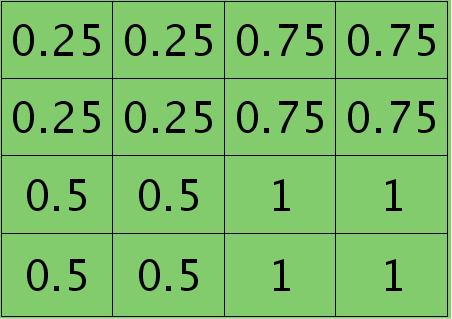
因为得满足反向传播时各层间误差敏感总和不变,所以卷积层对应每个值需要平摊(除以pooling区域大小即可,这里pooling层大小为2×2=4)),最后的卷积层值
分布为:
如果是max-pooling,则需要记录前向传播过程中pooling区域中最大值的位置,这里假设pooling层值1,3,2,4对应的pooling区域位置分别为右下、右上、左上、左下。则此时对应卷积层误差敏感值分布为:
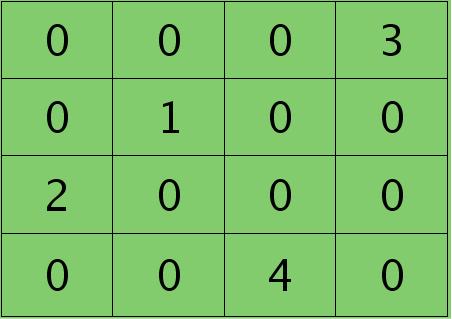
当然了,上面2种结果还需要点乘卷积层激发函数对应位置的导数值了,这里省略掉。
问题三:当接在pooling层的下一层为卷积层时,求该pooling层的误差敏感项。
假设第$l$层(pooling层)有$N$个通道,即有$N$张特征图,第$l+1$层(卷积层)有$M$个特征,$l$层中每个通道图都对应有自己的误差敏感值,其计算依据为第$l+1$层所有特征核的贡献之和。下面是第$l+1$层中第$j$个核对第$l$层第$i$个通道的误差敏感值计算方法:
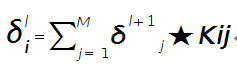
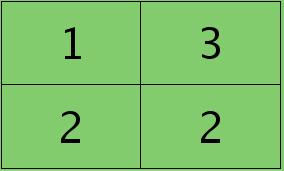
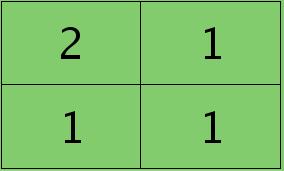
符号★表示的是矩阵的卷积操作,这是真正意义上的离散卷积,不同于卷积层前向传播时的相关操作,因为严格意义上来讲,卷积神经网络中的卷积操作本质是一个相关操作,并不是卷积操作,只不过它可以用卷积的方法去实现才这样叫。而求第i个通道的误差敏感项时需要将l+1层的所有核都计算一遍,然后求和。另外因为这里默认pooling层是线性激发函数,所以后面没有乘相应节点的导数。 举个简单的例子,假设拿出第$l$层某个通道图,大小为3×3,第l+1层有2个特征核,核大小为2×2,则在前向传播卷积时第$l+1$层会有2个大小为2×2的卷积图。如果2个特征核分别为:
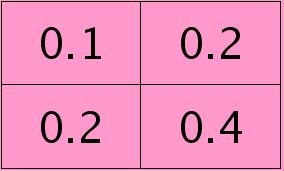
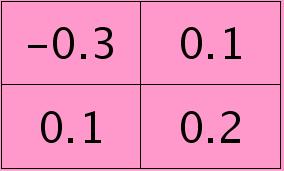
反向传播求误差敏感项时,假设已经知道第$l+1$层2个卷积图的误差敏感值:
离散卷积函数conv2()的实现相关子操作时需先将核旋转180度(即左右翻转后上下翻转),但这里实现的是严格意义上的卷积,所以在用conv2()时,对应的参数核不需要翻转(在有些toolbox里面,求这个问题时用了旋转,那是因为它们已经把所有的卷积核都旋转过,这样在前向传播时的相关操作就不用旋转了。并不矛盾)。且这时候该函数需要采用’full’模式,所以最终得到的矩阵大小为3×3,(其中3=2+2-1),刚好符第$l$层通道图的大小。采用’full’模式需先将第$l+1$层2个卷积图扩充,周围填0,padding后如下:
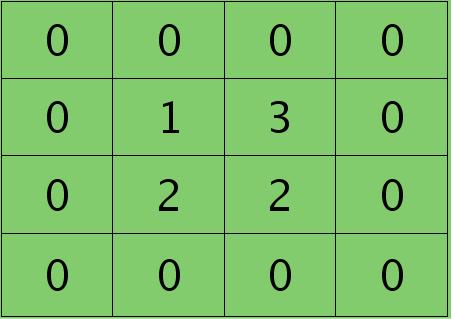
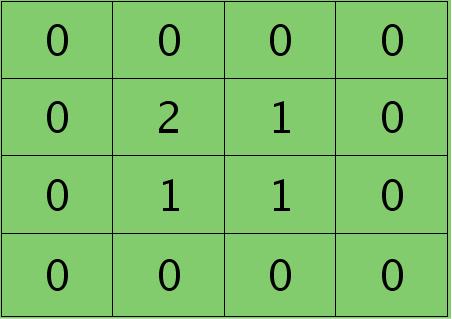
扩充后的矩阵和对应的核进行卷积的结果如下情况:
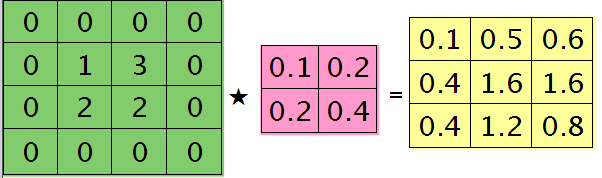
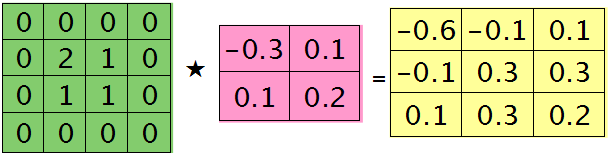
可以通过手动去验证上面的结果,因为是离散卷积操作,而离散卷积等价于将核旋转后再进行相关操作。而第$l$层那个通道的误差敏感项为上面2者的和,呼应问题三,最终答案为:

那么这样问题3这样解的依据是什么呢?其实很简单,本质上还是bp算法,即第$l$层的误差敏感值等于第$l+1$层的误差敏感值乘以两者之间的权值,只不过这里由于是用了卷积,且是有重叠的,$l$层中某个点会对$l+1$层中的多个点有影响。比如说最终的结果矩阵中最中间那个0.3是怎么来的呢?在用2×2的核对3×3的输入矩阵进行卷积时,一共进行了4次移动,而3×3矩阵最中间那个值在4次移动中均对输出结果有影响,且4次的影响分别在右下角、左下角、右上角、左上角。所以它的值为2×0.2+1×0.1+1×0.1-1×0.3=0.3, 建议大家用笔去算一下,那样就可以明白为什么这里可以采用带’full’类型的conv2()实现。
问题四:求与卷积层相连那层的权值、偏置值导数。
前面3个问题分别求得了输出层的误差敏感值、从pooling层推断出卷积层的误差敏感值、从卷积层推断出pooling层的误差敏感值。下面需要利用这些误差敏感值模型中参数的导数。这里没有考虑pooling层的非线性激发,因此pooling层前面是没有权值的,也就没有所谓的权值的导数了。现在将主要精力放在卷积层前面权值的求导上(也就是问题四)。
假设现在需要求第$l$层的第$i$个通道,与第$l+1$层的第$j$个通道之间的权值和偏置的导数,则计算公式如下:
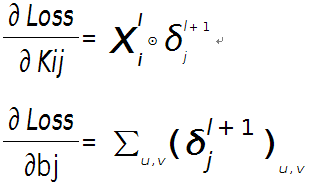
其中符号⊙表示矩阵的相关操作,可以采用conv2()函数实现。在使用该函数时,需将第$l+1$层第$j$个误差敏感值翻转。
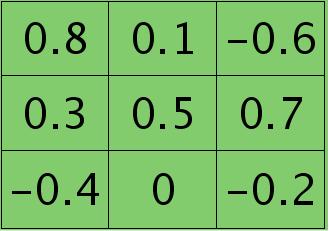
例如,如果第$l$层某个通道矩阵$i$大小为4×4,如下:
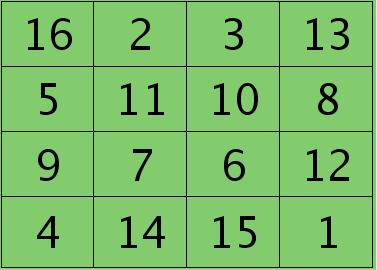
第$l+1$层第$j$个特征的误差敏感值矩阵大小为3×3,如下:
很明显,这时候的特征$K_{ij}$导数的大小为2×2的,且其结果为:
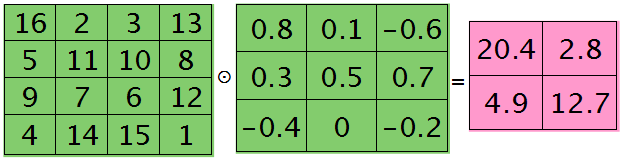
而此时偏置值$b_{j}$的导数为1.2 ,将$j$区域的误差敏感值相加即可(0.8+0.1-0.6+0.3+0.5+0.7-0.4-0.2=1.2),因为$b$对$j$中的每个节点都有贡献,按照多项式的求导规则(和的导数等于导数的和)很容易得到。
为什么采用矩阵的相关操作就可以实现这个功能呢?由bp算法可知,$l$层$i$和$l+1$层$j$之间的权值等于$l+1$层$j$处误差敏感值乘以$l$层$i$处的输入,而$j$中某个节点因为是由$i+1$中一个区域与权值卷积后所得,所以$j$处该节点的误差敏感值对权值中所有元素都有贡献,由此可见,将$j$中每个元素对权值的贡献(尺寸和核大小相同)相加,就得到了权值的偏导数了(这个例子的结果是由9个2×2大小的矩阵之和),同样,如果大家动笔去推算一下,就会明白这时候为什么可以用带’valid’的conv2()完成此功能。
接下来将单独写一篇博客解释为什么网络正向传播是feature map和卷积核相关(卷积)操作,而反向传播时候需要卷积(相关)操作
总结
反向传播过程中,如果前向传播使用的相关滤波器。反向传播时,针对当前层是卷积层时:
前一层的feature map的$\delta$值等于当前层feature map的$\delta$值卷积操作当前层的相关滤波器(或者表述为当前层feature map的$\delta$值相关操作前后左右翻转当前层的相关滤波器)。
当前层的滤波器$\delta$更新等于前一层的feature map的值和当前层feature map的$\delta$值的相关操作。
看我写的辛苦求打赏啊!!!有学术讨论和指点请加微信manutdzou,注明

